Que es el Interés Compuesto y como Funciona?
![]()
El interés compuesto es un principio financiero en el cual el interés generado por un capital inicial (inversión o préstamo) se reinvierte o acumula, de manera que, con el tiempo, los intereses también generan más intereses. Esto hace que el capital crezca a un ritmo más acelerado que con el interés simple, donde los intereses no se suman al capital inicial.
Fórmula del interés compuesto La fórmula general para calcular el interés compuesto es: A = P \cdot (1 + r)^n, Donde: – (A): Monto total al final del período. – (P): Capital inicial (inversión o préstamo). – (r): Tasa de interés por período (en decimal: por ejemplo, 5% = 0,05). – (n): Número de períodos en los que se acumula el interés. Si el interés compuesto se calcula con más frecuencia que una vez al año (mensual, diario, etc.), la fórmula se adapta a: [ A = P \cdot \left(1 + \frac{r}{m}\ right)^{n \cdot m} ] Donde: – (m): Número de veces que el interés se capitaliza por año. Ejemplo práctico Imagina que invierte $1,000 USD con una tasa de interés del 5% anual, capitalizada anualmente, durante 3 años. 1. Usando la fórmula: [ A = 1000 \cdot (1 + 0.05)^3 ] [ A = 1000 \cdot (1.157625) = 1157.63 \, \text{USD} ]
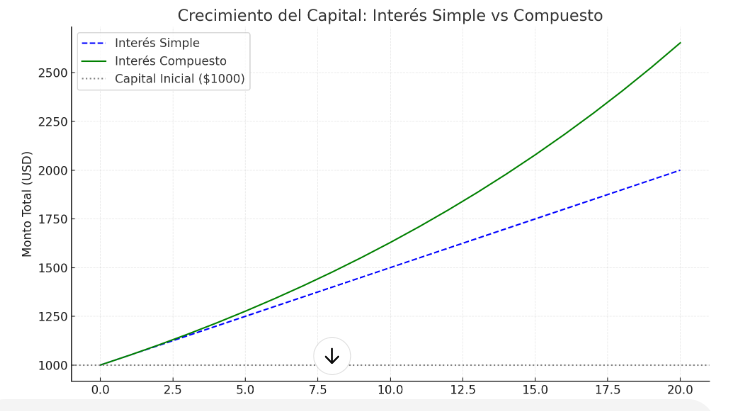
Aquí tienes una imagen explicativa sobre el interés compuesto, acompañada de un gráfico ilustrado.
El Poder del Interés Compuesto: Crecimiento Exponencial en las Finanzas
¿Cómo funciona
Ejemplos prácticos
Supongamos que invierte $1,000 USD a una tasa del 5% :
- Con interés simple ,$2,000 dólares .
- Con Interés Compuesto ,$3,386 USD , casi un 7070% más que lo simple
¿Estás listo para aprovechar su poder? ¡Empieza hoy! El interés compuesto funciona y tiene un efecto como la bola de nieve.
1. Capital inicial (inversión o préstamo)
capital inicial .$1,000 USD a un 5% de utilidad
2. Intereses generados
En el primer mes del primer año=1000×0.05=50 USD.\Interés del primer año = 1000 \times 0.05 = 50 Interés del primer año=1000×0.05=50USD.
3. Reinversión de intereses
En el segundo período, el interés ya no se calcula solo sobre los $1,000 USD originales, sino sobre el total acumulado, que ahora es $1,050 USD (capital + intereses del primer año). Esto genera más Interés del segundo año=1050×0.05=52.50 USD.Interés del segundo año = 1050 \times 0.05 = 52.50 \,USD.Intereˊs del segundo an˜o=1050×0.05=52.50USD.
El1050+52,50=1102.50 Dólar estadounidense.1050 + 52,50 = 1102,50 \, \text{USD}.1050+52,50=1102.50DÓLAR ESTADOUNIDENSE .
4. Crecimiento exponencial
A medida que pasan los años, los intereses acumulados generan cada vez más intereses. Con el tiempo, esto crea una curva de crecimiento exponencial , en la que el capital crece más rápido cuanto más tiempo se mantiene invertido.
Fórmula en acción
Si quieres calcular rápidamente el valor final después de varios períodos, utiliza esta fórmula:A=PAG⋅(1+a)norteA = P \cdot (1 + r)^nA=PAG⋅( 1+o )norte
- AAA: Monto total después de nortenortenorte Períodos.
- PAGPAGPAG: Capital inicial.
- aaa: Tasa de interés por período.
- nortenortenorte: Número de períodos.
Ejemplo práctico con 5 años
Si invierte $1,000 USD al 5% anual durante 5 años:A=1000⋅(1+0,05)5=1000⋅1.27628=1276.28 Dólar estadounidense.A = 1000 \cdot (1 + 0,05)^5 = 1000 \cdot 1,27628 = 1276,28 \, \text{USD}.A=1000⋅( 1+0,05 )5=1000⋅1.27628=1276.28DÓLAR ESTADOUNIDENSE .
El capital creció $276.28 USD gracias al interés compuesto.
Importancia del tiempo
El interés compuesto recompensa a quienes son pacientes:
- Si duplicas el tiempo (de 5 a 10 años), no solo duplicas las ganancias: ¡las multiplicas!
- En 10 años con la misma inversión, el total sería:
A=1000⋅(1+0,05)10=1000⋅1.62889=1628,89 Dólar estadounidense.A = 1000 \cdot (1 + 0,05)^{10} = 1000 \cdot 1,62889 = 1628,89 \, \text{USD}.A=1000⋅( 1+0,05 )10=1000⋅1.62889=1628,89DÓLAR ESTADOUNIDENSE .
Conclusión
El interés compuesto es más efectivo en cuanto:
- Mayor sea el tiempo de inversión.
- Mayor sea la tasa de interés.
- Más frecuentemente se capitalice (mensual, diario, etc.).
Es una herramienta clave en la acumulación de riqueza a largo plazo.












